DFA (Deterministic Finite Automata)
이제부터 전자계산기의 동작을 알아보도록 하자.
DFA는 이름에서 알 수 있듯 "결정적인 유한 오토마타"이다.
상태는 유한하고 어떤 상태에서 어떤 입력이 들어오면 이동하는 상태가 정해져있다는 뜻이다.
DFA 는 다음으로 이루어져있다.
$ M = (Q, \Sigma, q, F, s)$
- $Q$ : DFA상태들의 집합
- $\Sigma$ : 입력받은 String
- $q$ : 초기상태 ($q \in Q$)
- $F$ : AC를 받는 상태들의 집합 ($F \in Q$, 여러개 가능)
- $s$ : Transition Function
표기법은 책, 자료마다 다르지만 의미는 같다.
지난시간에 본 Problem X1을 DFA로 나타내면 다음과 같다.

여기에서 각 노드(원)가 $Q$들이다.
$q$는 start와 연결된 노드
$F$는 오른쪽에 있는 두개의 원이 겹쳐진 노드
$s$는 숫자가 적혀있는 화살표들이다.
여기에서 $\Sigma$로 011이 들어온다면 오른쪽 $\rightarrow$ 왼쪽 $\rightarrow$ 왼쪽 으로 끝나게 된다.
반면 10이 들어온다면 왼쪽 $\rightarrow$ 오른쪽 으로 끝나게 된다.
011은 $F$에서 끝나지 않아서 AC받지 못하고, 10은 $F$에서 끝나므로 AC를 받게 된다.
AC를 받으면 YES, 아니라면 NO이기 때문에 Decision Problem이 된다.
또 다른 예시를 들어보자.
Problem X3 : 입력에 101이 있는가?
X3의 정답은 $L3 = \{101, 0101, 1010, 01010, \dots \}$가 될 것이다.
이를 DFA로 나타내면 다음과 같다.

하지만 다음과 같은 예시를 보자
Problem X5 : $L5 = \{x|x=0^i1^i, 0 \le i\}$, 여기서 $a^2 = aa$이다.
일단 문제를 간소화 해서 $L5_0 = \{x|x=0^i1^i, 0 = i \}$을 보자.
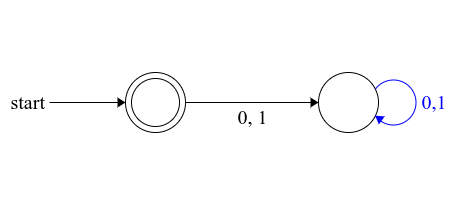
위와 같이 간단하게 나온다.
마찬가지로 $L5_1, L5_2$는 아래와 같다.
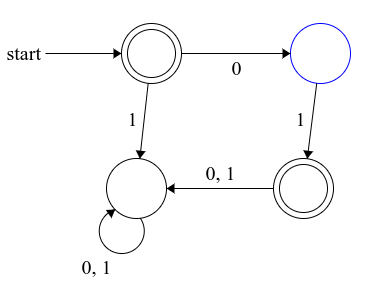
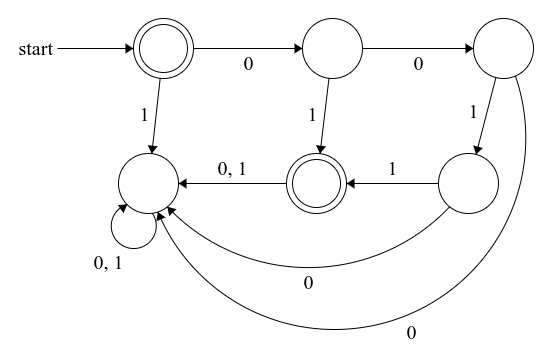
$L5_i$일 때마다 상태의 수가 $2(i+1)$개가 된다.
$L5$는 임의의 $i$에 대해 AC를 해야 하므로 $i$가 무한히 커지면 상태의 수도 같이 무한히 커지게 된다.
이는 DFA에서 Finite에 위배되므로 Problem X5를 해결하는 DFA는 존재하지 않는다.
DFA가 Problem X5를 해결할 수 없다는 증명이 있는데 이는 다음시간에 알아보도록 한다.
연습문제
Problem X4 : $L4 = \{x|x=0^i1^j, 0\le i,j\}$, 여기서 $a^2 = aa$이다.
Problem X4를 AC하는 DFA는 존재하는가?
존재한다면 그 DFA를 그려보자!
'기타 > 암호학' 카테고리의 다른 글
| [암호학] 9. Non-Deterministic Finite Automata (NFA) (0) | 2022.12.27 |
|---|---|
| [암호학] 8. Pumping Lemma, Pigeonhole Principle (2) | 2022.12.23 |
| [암호학] 6. 프로그래밍 언어론 (4) | 2022.12.16 |
| [암호학] 5. 집합론 2 (0) | 2022.12.13 |
| [암호학] 4. 집합론 1 (0) | 2022.12.09 |