자 이쯤되면 필요한 배경지식은 모두 쌓은것 같네요. 이제 암호학을 배우러 가보도록 하죠
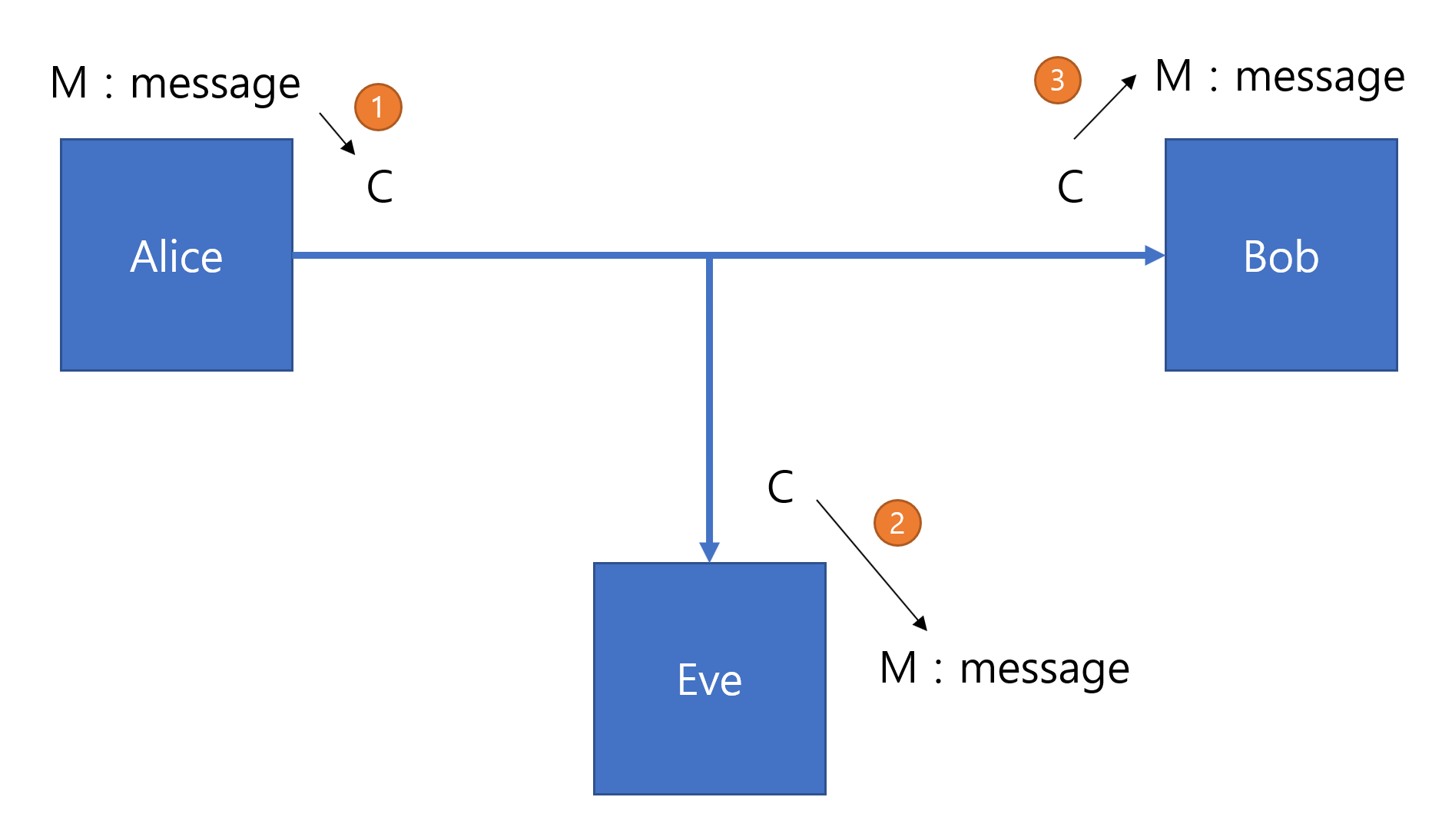
첫 시간에 봤던 그림이다.
M -> C로 암호화하는 Problem X1가 있을 것이고 C -> M으로 복호화하는 Problem X2가 있을 것이다.
즉 위 그림에서 1번에 X1이 들어가고, 2와 3번에 X2가 들어간다.
그럼 가장 베스트인 경우는 2는 해결할 수 없고 3은 해결할 수 있으면 좋을 것이다. (1은 언제나 해결 가능해야 함..)
그것이 가능할까?
Solvable vs Unsolvable
Solvable은 말 그대로 해결할 수 있는 Problem, Unsolvable은 해결할 수 없는 Problem이다.
Class D에 포함되는 Problem들은 Solvable하다. (Yes, No가 출력으로 나오니까..)
반면 Halting Problem은 Class D 밖에 있기 때문에 Undecidable하고 해결할 수 없는 문제라고 했기 때문에 Unsolvable이라고 말할 수 있다.
이상적인 암호
위에서 말했듯 이상적인 암호는 2는 Unsolvable, 3은 Solvable하길 원한다.
하지만 모든 Turing Machine의 성능은 같기 때문에 3이 해결된다면 2도 어떻게해서든 해결할 수 있다.
시간은 오래걸릴 수 있지만 시도해본다면 답이 뭔진 몰라도 나오게 된다!
가장 단순하게 말해서 password를 뚫기 위해 모든 경우를 시도하면 정답은 적어도 한번 도출하게 된다는 것이다.
예를들어 password가 123이면 비밀번호가 1자리수, 2자리수, 3자리수... 인 모든 경우를 시도해본다.
가능한 경우가 아스키코드 개수 128개(실제로는 더 적을 것이다.) ^ 비밀번호 자릿수 번만 시도하면 123을 얻을 수 있게 된다.
만약 자신이 해커이고 공격하려는 비밀번호가 10자리라는 것을 알고있다고 하자. (몰라도 큰 상관은 없다.)
해당 비밀번호가 알파벳 소문자로만 이루어져 있다면 $26^{10}$번만 시도하면 된다.
알파벳 소문자 + 대문자로 이루어져 있다면 $52^{10}$번만 시도하면 된다.
알파벳 소문자 + 대문자 + 숫자로 이루어져 있다면 $62^{10}$번 시도하면 된다.
알파벳 소문자 + 대문자 + 숫자 + 특수문자(약 15개)로 이루어져 있다면 $77^{10}$번 시도하면 된다.
...
조합이 다양해질수록 시도횟수가 크게 늘어난다.
그래서 보통의 웹사이트에서 다양한 조합으로 긴 패스워드 사용을 권장하는 것이다.
대부분의 웹사이트는 이런 상황을 방지하기 위해 5회 이상 패스워드 틀릴 시 아이디 잠금 기능이 있다.
위의 경우는 하나의 예시이고 암호화, 복호화하는 Problem은 무엇이든 될 수 있다.
예를들어 3번이 최단경로 문제를 해결하면 M을 얻을 수 있다고 하자. (더 일반적으로 백준이나 코드포스에 있는 모든 알고리즘 문제가 될 수 있다.)
그렇다면 2번도 해당 문제를 해결하면 얻을 수 있다.
다익스트라같은 특정 알고리즘을 모른다면 $O(n!)$로 모든 경우를 시도할 수 있다.
시간은 오래걸리겠지만 해결할수는 있다는 것이다. (이는 알고리즘분야가 중요한 이유이기도 하다.)
그럼 시간이 무한한 경우가 걸림돌이 되므로 시간을 제한하면 되잖아요?
아주 좋은 방법이다.
패스워드를 입력하는 창이 나오고 1분안에 해결하지 못하면 문제가 바뀌는 식으로 구성하면 될 것이다.
따라서 다음시간부터 시간을 제한한 Problem들을 다룰 것이다.
'기타 > 암호학' 카테고리의 다른 글
| [암호학] 17. P, NP (0) | 2023.01.24 |
|---|---|
| [암호학] 16. Complexity Classes (0) | 2023.01.20 |
| [암호학] 14. Classes 2 (0) | 2023.01.13 |
| [암호학] 13. Classes 1 (0) | 2023.01.10 |
| [암호학] 12. Turing Machine (0) | 2023.01.06 |