P=NP는 수십년동안 해결되지 않은 난제로 남아있다.
위 문제가 암호에 관련이 있다고 하는데 어떤 연관이 있는지 알아보자.
NP Class
전 시간에 $NP$는 NTM이 다항시간에 해결하는 Problem 집합이라고 했다.
이와 다르게 $NP$를 정의할 수 있다.
$NP$는 DTM에게 적절한 힌트를 주면 YES를 검증할 수 있거나 다항시간에 해결할 수 있는 Problem 집합이다.
NP-Complete라고 했던 Longest Path 문제를 보자.
단순히 그래프를 주고 A -> B로 가는 가장 긴 경로를 출력하라고 하면 힘들것이다.
하지만 문제를 그래프를 주고 A -> B로 가는 k이상의 경로가 있는가?로 바꾼다면 검증할 수 있다.
그러한 경로를 보여주면 된다!
Longest Path문제도 그런 경로를 보여주면 되는거 아닌가요?
만약 Longest Path문제에서 가장 길다고 생각하는 경로를 찾았다면 그보다 긴 경로가 없음을 보여야 한다.
위의 정의에서 YES는 검증할 수 있다고 말했지만 NO는 검증하기 힘들다.
즉, 위의 예시에서 hint는 K라는 특정 거리이고 이를 통해 $P$로 바꿀 수 있음을 알 수 있다.
암호에서의 활용
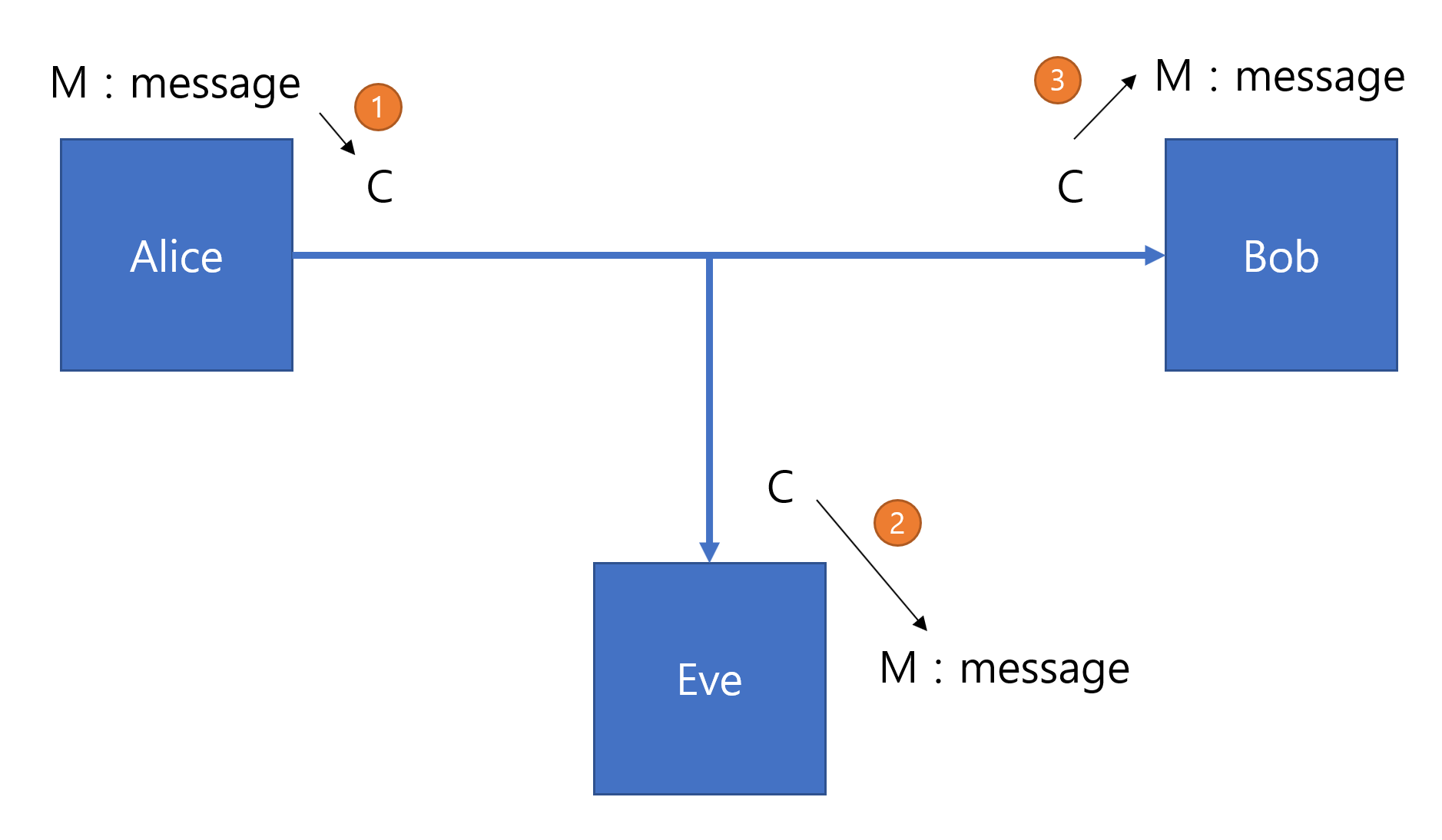
전에 나왔던 그림인데 다시 한번 보자.
1번은 해결할 수 있는 어떤 문제가 와도 좋다. (해결할 수 없으면 암호화가 되지 않는다.)
2, 3번은 같은 문제이지만 2번에게는 해결할 수 없고 3번은 해결할 수 있도록 하고 싶다.
하지만 그렇게 설계할 수 없다고 했으므로 나왔던 대안이 시간을 제한하는 것이었다.
3번은 $P$, 2번은 $NP$이상이면 좋을 것 같다. 그렇게 되면 3은 빠르게 해결하고 2는 느리게 해결하여 시간 내에 해결할 수 없기 때문이다. (알고리즘 문제에서 시간 제한을 생각하면 된다. 3번도 $NP$이상이라면 복호화를 하는데 오래 걸린다.)
우선 지난시간 $P \neq EXP$라고 했으므로 3번을 $P$로 한다는건 2번은 오래걸려야 $NP$까지 가능하다.
즉, 3번은 $P$, 2번은 $NP$가 되도록 설계할 수 있다면 쓸만한 암호를 만들 수 있다.
그러나
$P \neq NP$라면 위에서 말한 쓸만한 암호를 만들 수 있다.
$P = NP$라면 3이 해결할 수 있는 문제를 2도 3과 같은 속도로 해결할 수 있기 때문에 안전한 암호가 될 수 없다.
위와 같은 이유로 P=NP가 증명되면 암호를 모두 갈아치워야 하는 상황이 발생한다.
대안
그렇다고 암호를 아예 못쓰는 건 아니다.
Bob에게 적절한 힌트를 줘서 빠르게 해결하게 하고 Eve에게는 힌트를 주지 않아 느리게 해결하게 만들면 된다.
힌트가 있으면 문제가 $O(n^2)$에 해결되고 없을 때 $O(n^{100})$에 해결된다면 그나마 사용할 수 있다. ($N$이 10만 되더라도 $O(n^{100})$이면 $10^{100}$이다!)
일상에서의 예시
Alice가 사물함을 자물쇠로 잠갔다. (암호화)
Alice는 Bob에게 자물쇠를 푸는 열쇠를 전달한다. (Hint 제공)
Bob은 그 열쇠로 사물함을 쉽게 열 수 있다. (빠른 속도의 복호화)
Eve는 같은 사물함에 있는 자물쇠를 열기 위해 자물쇠를 분석하고 거기에 알맞는 열쇠를 제작하여 열 수 있다. (느린 속도의 복호화)
하지만 위의 예시에서 문제점이 하나 있다.
바로 Hint를 제공하는 과정에서 Hint를 빼앗길 수 있다는 것이다.
실용적이진 않지만 이런 문제를 해결하는 방법을 뒤에서 알아볼 예정이다.
'기타 > 암호학' 카테고리의 다른 글
| [암호학] 19. RSA 암호 (0) | 2023.01.31 |
|---|---|
| [암호학] 18. NP-Complete (0) | 2023.01.27 |
| [암호학] 16. Complexity Classes (0) | 2023.01.20 |
| [암호학] 15. 암호란 무엇인가? 2 (0) | 2023.01.17 |
| [암호학] 14. Classes 2 (0) | 2023.01.13 |