소인수분해를 하는 가장 쉬운 방법은 약수를 구하듯이 $\sqrt N$까지 검사하며 나누어질 경우 인수로 가져가는 방식이 있을 것이다. 이러한 방법도 괜찮지만 $N \le 10^{18}$정도 된다면 TLE가 나는 느린 방법이다. 위 방법의 시간복잡도는 $\sqrt N$이지만 입력이 숫자이기 때문에 복잡도상으로 보면 지수시간을 가지는 느린 알고리즘이다. 소인수분해는 그만큼 어려운 문제이기 때문에 암호에도 많이 쓴다. 위 방법보다 빠르고 $10^{18}$범위까지 해결할 수 있는 Pollard rho 알고리즘에 대해 알아보자.
Pollard rho를 이해하기 위해 몰라도 되지만 알면 좋은 사전지식이 있다.
Birthday Paradox
사람들이 얼마나 모여야 생일이 같은 사람이 존재할 수 있을까?
비둘기집의 원리에 의하면 윤년이 아닌 경우 366명만 모이면 무조건 존재한다. 하지만 이건 너무 재미없기 때문에 다음 문제를 생각해보자.
사람들이 얼마나 모여야 생일이 같은 사람이 존재할 확률이 50%를 넘을 수 있을까?
이제 좀 흥미롭다. 단순한 계산을 통해 위 문제를 해결할 수 있다. $k$명의 사람들이 모였을 때 생일이 겹치는 경우가 있을 확률을 $Q_k$, 생일이 겹치는 경우가 없는 확률을 $P_k$라고 하자. $Q_k + P_k = 1$이다. 여기에서 $P_k$를 구하는 것은 쉽다. 1년의 일 수를 $n$이라고 하자. 적절한 조합을 사용하면 $P_k = \frac{n(n-1)(n-2)\cdots(n-k+1)}{n^k} = \prod_{i=0}^{k-1} (1 - \frac{i}{n})$임을 알아낼 수 있다.
여기에서 $1 + x \le e^x$라는 사실을 사용하자.
$P_k \le \prod_{i=0}^{k-1} e ^ {-\frac{i}{n}} = e^{\sum_{i=0}^{k-1} -\frac{i}{n}} = e^{-\frac{1}{n} \frac{k(k-1)}{2}}$ 라는 사실을 얻을 수 있다. 우리가 원하는 것은 $Q_k \ge \frac{1}{2}$인 $k$를 찾는 것이므로 $P_k \le \frac{1}{2}$인 $k$를 찾는 것과 같다.
$e^{-\frac{1}{n} \frac{k(k-1)}{2}} \le \frac{1}{2} = e^{ - \ln 2}$
$\frac{1}{n} \frac{k(k-1)}{2} \ge \ln 2$
$k^2 - k - 2n \ln 2\ge 0$
$k = \frac{1 \pm \sqrt{1+8n \ln 2}}{2}$를 경계로 하고 음수가 될 수는 없으므로 $k \ge \frac{1 + \sqrt{1+8n \ln 2}}{2}$이라면 생일이 같은 사람이 존재할 확률이 50%가 넘게 된다. $n = 365$를 넣어 계산하면 $k \ge 22.9999431 \dots$이 나오게 된다. 즉, 23명만 모여도 생일이 같은 사람이 존재할 확률은 50%가 넘게 된다.
사실 위의 디테일한 계산은 중요하지 않고 Birthday Paradox에서 중요한 것은 생각보다 적은 표본으로도 겹칠 확률이 충분히 높다는 사실이다.
토끼와 거북이 알고리즘
알고리즘 이름이 귀엽다. 플로이드의 tortoise & hare algorithm이라고 알려진 이 알고리즘은 connected functional graph에서 사이클이 시작하는 노드를 찾는 알고리즘이다. 여기서 functional graph는 모든 노드의 나가는 간선이 오직 한 개인 그래프이다. 보통의 알고리즘 문제라면 indegree가 2인 노드를 찾으면 되기 때문에 굉장히 쉽게 풀리지만 Pollard rho에서는 중요하게 쓰인다. 그래프 전체가 사이클이라면 사이클의 시작 노드를 찾을 수 없기 때문에 전체가 사이클이면 안된다. 알고리즘은 다음과 같다.
- indegree가 0인 노드에 $A, B$를 둔다.
- $A$는 간선을 따라 2칸씩 이동하고 $B$는 1칸씩 이동한다.
- 2번을 반복하다보면 두 포인터는 어떤 노드에서 만나게 된다. 이 때 $A$는 indegree가 0인 노드로 옮기고 $B$는 그대로 둔다.
- $A$와 $B$가 만날때까지 간선을 따라 1칸씩 이동한다.
- 둘이 만난 노드가 사이클이 시작하는 노드이다.
시간복잡도는 $O(N)$이다.
이제 사전지식은 끝났고 Pollard rho 알고리즘을 알아보자.
기본적인 아이디어는 합성수 $N$이 주어졌을 때 어떠한 방법으로 $N$의 약수 $v$를 구하여 $\frac{N}{v}, v$에 각각 동일한 알고리즘을 적용하여 소인수분해를 진행하는 방식이다. 여기에서 그 어떠한 방법을 알아보자.
Naive
$2 \le x \le N$를 랜덤하게 뽑아 $\gcd(x, N) > 1$가 된다면 괜찮은 확률로 $v = \gcd(x, N)$인 약수를 구할 수 있다. 이를 사용하여 작은 수의 소인수분해를 해결할 수 있다.
Pollard rho
우선 2차 이상의 단순한 다항식을 하나 선택한다. 1차 다항식은 알고리즘 속도가 너무 느려지기때문에 고려하지 않는다. 보통 차수가 높으면 속도가 계산하느라 느려질 수 있으므로 단순한 2차로 선택한다.
$f(x) = x^2 + c$
$c \neq 0$이 좋은데 계산하다가 값이 $0$이 나와버리면 그대로 무한루프에 빠지기 때문이다.. 그리고 $0 \le x_0 \le N - 1$을 선택한다. 그렇게 $x_{i+1} = f(x) \mod N$을 수행하면 언젠가 $x_i = x_j \mod N$인 지점이 생긴다.
예를 들어 $N = 10, x_0 = 3, f(x) = x^2 +1$라고 하자. 수열 $x_n = \{3, 0, 1, 2, 5, 6, 7, 0, \dots\}$가 생기게 되고 이를 그래프로 표현하면 다음과 같다.
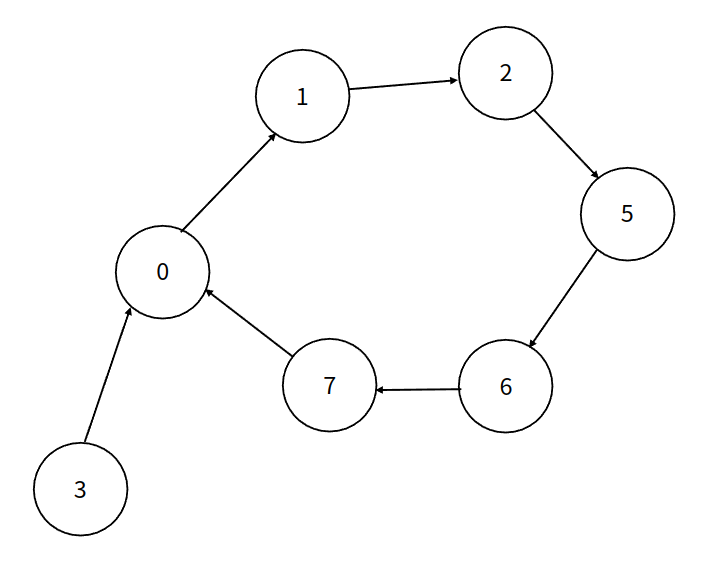
이 모양이 그리스어 $\rho$(rho)같이 생겼다고 해서 Pollard rho라는 이름이 붙었다. 그럼 여기서 의문이 생긴다.
수가 엄청 크면 rho의 크기도 엄청 커질 것 같은데?
$f$를 통과할때마다 적당한 난수가 추출되므로 Birthday Paradox에 의하면 표본이 꽤 적어도 겹치는 수가 나올 확률이 높다. 하지만 $f$로 1차 다항식을 선택하면 Birthday Paradox와 관계없이 rho크기는 커진다!
이제 $x_i, x_j$를 보며 $v = \gcd (|x_i - x_j|, N) > 1$인지 본다.
$v = N$이라면 $x_0, c$를 다시 정해 처음부터 다시 시작한다.
$v < N$이라면 Naive때와 마찬가지로 약수를 하나 구한 것이므로 $\frac{N}{v}, v$에 대해 알고리즘을 각각 재귀적으로 수행한다.
구해진 rho 크기를 $P$라고 하자. Birthday Paradox에 의해 $P$가 적당히 작다는 것은 알지만 모든 $x_i, x_j$에 대해 확인하는 방법은 $O(P^2)$의 시간이 걸리므로 비효율적이다. 그래서 적당히 $j = 2i$를 선택하여 $x_i, x_{2i}$만 확인하여 체크하는 방법이 좋다. 이 방법의 좋은 점은 토끼와 거북이 알고리즘에 의해 $O(P)$번 안에 무조건 같은 노드에 도착하게 된다는 사실이 보장된다. 같은 노드에 도착하게 되면 $v = \gcd(0, N) = N$이므로 처음부터 다시 시작하게 된다.
시간복잡도는 복잡한 분석에 의해 $O(N^\frac{1}{4})$로 알려져있다. 이는 $N \le 10^{18}$인 경우에도 해결할 수 있을 정도로 충분히 빠르다.
주의할 점으로 소수를 대상으로 Pollard rho를 수행하게 되면 무한루프에 빠지므로 각 step 시작하기 전에 소수인지 판별해야한다. 여기에서 $O(\sqrt{N})$ 소수판별법을 사용하면 병목이 있으므로 충분히 빠른 이런 방법이나 밀러라빈 소수판별법등을 사용하도록 하자.
Pollard rho 연습문제
https://www.acmicpc.net/problem/4149
Reference
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] Splay Tree를 사용해서 해결할 수 있는 유형 (2) | 2024.10.24 |
|---|---|
| [알고리즘] PS를 위한 Splay Tree (1) | 2024.10.03 |
| [알고리즘] Suffix Automaton (0) | 2024.09.09 |
| [알고리즘] Push Relabel 알고리즘 (2) | 2024.08.30 |
| [알고리즘] Berlekamp-Massey 알고리즘 톺아보기 (2) | 2024.07.24 |