가장 쉬운 문자열 자료구조나 알고리즘은 무엇일까? 아마 트라이정도가 있을 것이다. 이런 트라이도 상당히 고난이도의 자료구조에 속하기 때문에 문자열을 사용하는 자료구조나 알고리즘은 많이 어렵다. 문자열의 꽃이라고 볼 수 있는 Suffix 자료구조도 굉장히 고난이도에 속한다. 우리나라에서는 Suffix Array나 Suffix Tree (Suffix Trie) 등이 알려져있지만 Suffix Automaton은 잘 알려져있지 않다. 여기에서는 엄밀한 증명은 제외하고 Suffix Automaton이 무엇인지 알아보도록 한다.
Automaton
이름에서 볼 수 있듯이 Suffix Automaton은 어떤 문자열의 Suffix로 Automaton을 그린 것이다. Automaton가 뭔지 모른다면 여기를 참고하자. Suffix Automaton도 DFA 구조로 되어있고 해당 문자열의 모든 Suffix를 Accept할 수 있다. 따라서 어떤 문자열 $T$가 다른 문자열 $S$의 부분문자열인지 확인하려면 $S$에 대한 Suffix Automaton을 구성하고 $T$를 Accept하는지 확인하면 된다. Suffix Automaton은 DFA이긴 하나 사이클이 없다. 그래서 DAG로 봐도 무방하다.
Endpos
Endpos는 Suffix Automaton에서 중요한 개념 중 하나이다. 문자열 $S$가 있을 때 $Endpos(T)$는 $S$에서 $T$가 등장하는 $S$에서의 마지막 위치 인덱스의 집합이다. 예를 들어 $S = ababa, T = ba$가 있다고하자. $Endpos(T)$를 구하면 $Endpos(T) = \{2, 4\}$가 된다. (0-based index) 또한 동일한 $Endpos$를 가지는 다른 문자열이 존재할 수 있다. 예를들어 $T=aba$가 되더라도 $Endpos(T) = \{2, 4\}$로 동일하다. 여기에서 $T_1 \neq T_2$이면서 $Endpos(T_1) = Endpos(T_2)$라면 $T_1, T_2$는 같은 상태에 있다고 한다. 여기에서 상태는 Automaton의 한 정점이다.
그럼 Endpos의 특징에 대해 알아보자.
- $S$의 substring $T_1, T_2$에 대해 $len(T_1) \le len(T_2)$이고 $T_1, T_2$가 같은 상태에 있다면 $T_1$은 $T_2$의 suffix이다.
부분문자열의 길이가 길어질수록 $Endpos$의 크기가 커지지 않는다는 것은 자명하다. $Endpos$의 정의에 따라 끝 위치는 동일한데 길이가 길어졌으므로 $T_1$은 $T_2$의 suffix가 된다.
- $S$의 substring $T_1, T_2$에 대해 $len(T_1) \le len(T_2)$일 때 $Endpos(T_2) \subseteq Endpos(T_1)$라면 $T_1$은 $T_2$의 suffix이고, $Endpos(T_1) \cap Endpos(T_2) = \varnothing$이라면 $T_1$은 $T_2$의 suffix가 아니다.
첫 번째 특징의 확장판이다. suffix 조건부터 보면 $T_2$가 가지고 있는 모든 $Endpos$를 $T_1$도 가지기 때문에 suffix임을 쉽게 알 수 있다. 즉, $T_1$의 모든 suffix를 $T_2$도 가지고 있다. 그렇지 않다면 $T_1$과 $T_2$에는 같은 suffix가 없을 수 있다는 것으로 $T_1$은 $T_2$의 suffix가 될 수 없다.
$S = ababa$에서 중복을 제외한 부분문자열을 모두 모아보면 $T = \{a, b, ab, ba, aba, bab, abab, baba, ababa\}$가 나온다. 각 부분문자열의 $Endpos$를 구해보자.
- $Endpos(a) = \{0, 2, 4\}$
- $Endpos(b) = \{1, 3\}$
- $Endpos(ab) = \{1, 3\}$
- $Endpos(ba) = \{2, 4\}$
- $Endpos(aba) = \{2, 4\}$
- $Endpos(bab) = \{3\}$
- $Endpos(abab) = \{3\}$
- $Endpos(baba) = \{4\}$
- $Endpos(ababa) = \{4\}$
이제 위 특징들이 보이는가? $Endpos$가 다른 부분문자열의 $Endpos$의 부분집합이면 suffix인 것을 볼 수 있다. 그리고 $\{b, ab\}, \{ba,aba\}, \{bab,abab\}, \{baba,ababa\}$같이 $Endpos$가 같은 부분문자열도 있으며 각 원소들은 가장 긴 원소의 suffix인 것도 확인할 수 있다. $S$로 suffix automaton을 구성한다면 상태는 5개가 나오게 된다. (루트 상태 제외) $S$의 suffix automaton은 다음과 같다.
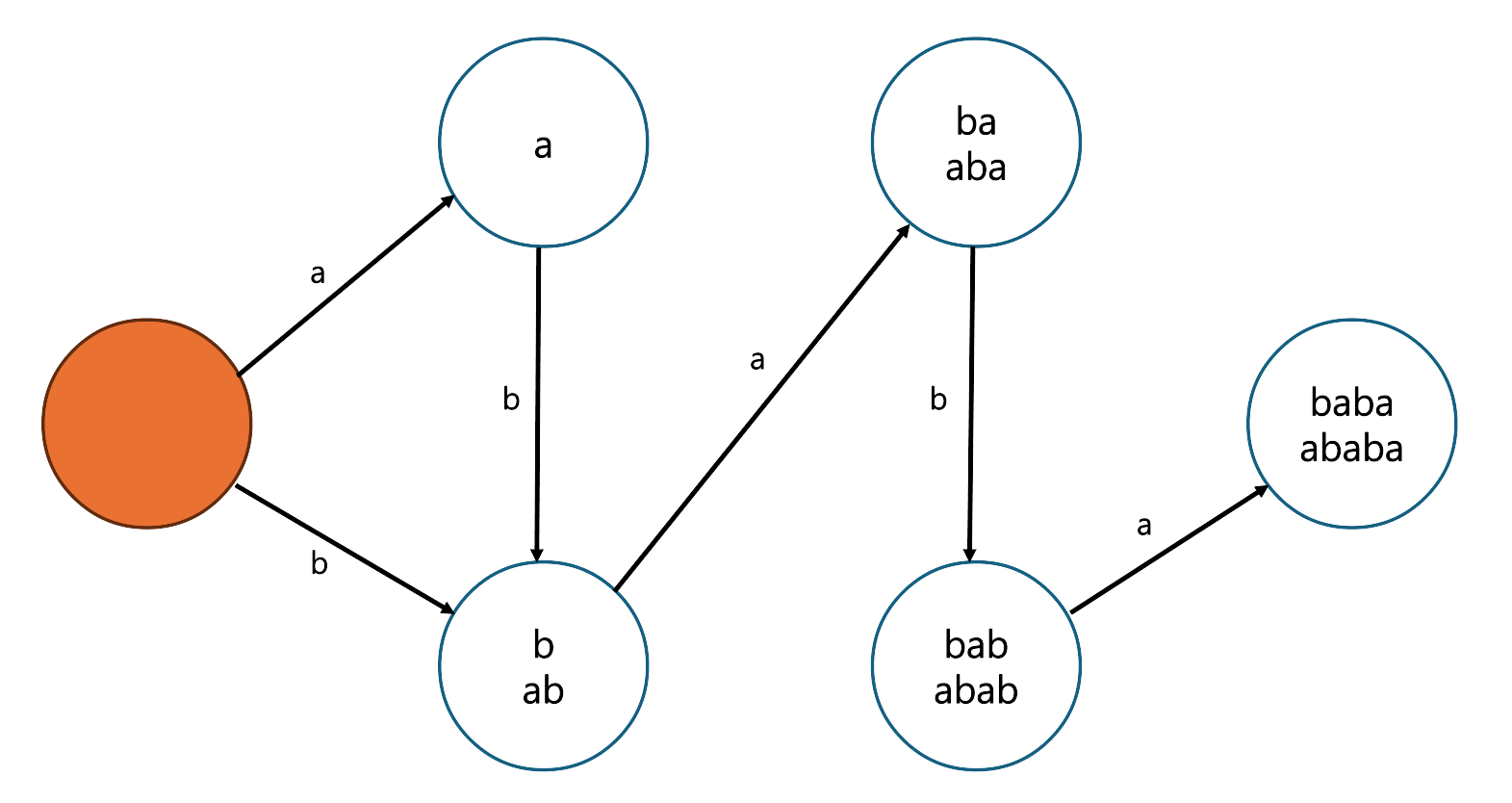
같은 $Endpos$를 가지는 부분문자열은 같은 상태를 가지고 각 간선을 문자열 맨 뒤에 추가하며 따라가면 해당 상태에 있는 문자열 중 하나가 만들어진다. 그럼 suffix automaton을 구하기 위해 모든 부분문자열[$O(N^2)$]의 $Endpos$를 구해서[$O(N)$] 연결시키면 suffix automaton을 구성하는 $O(N^3)$알고리즘을 생각할 수 있다. 하지만 이는 대부분의 제한에서 실용성 없는 알고리즘이고 $O(N \log N)$인 suffix array를 사용하는 것이 훨씬 나을 수 있다. 더 빠르게 suffix automaton을 구성하기위해 suffix automaton의 꽃인 suffix link라는 개념을 도입한다.
Suffix Link
suffix link의 개념은 간단하다. 단순히 현재 상태의 $Endpos$를 부분집합으로 가지는 가장 작은 크기의 $Endpos$를 가지는 상태로 연결하는 간선이다. 상태 $v$의 suffix link를 $link(v)$라고 하면 $Endpos(v) \subset Endpos(link(v))$이다. 예를들어 $Endpos(ababa) = \{4\}$가 있을 때 $Endpos(a) = \{0, 2, 4\}, Endpos(ba) = \{2, 4\}$ 둘 다 부분집합으로 가질 수 있기때문에 가장 작은 $Endpos$상태인 $\{ba, aba\}$로 간선을 뻗어주면 된다.
suffix link를 추가한 $S$의 suffix automaton은 다음과 같다.
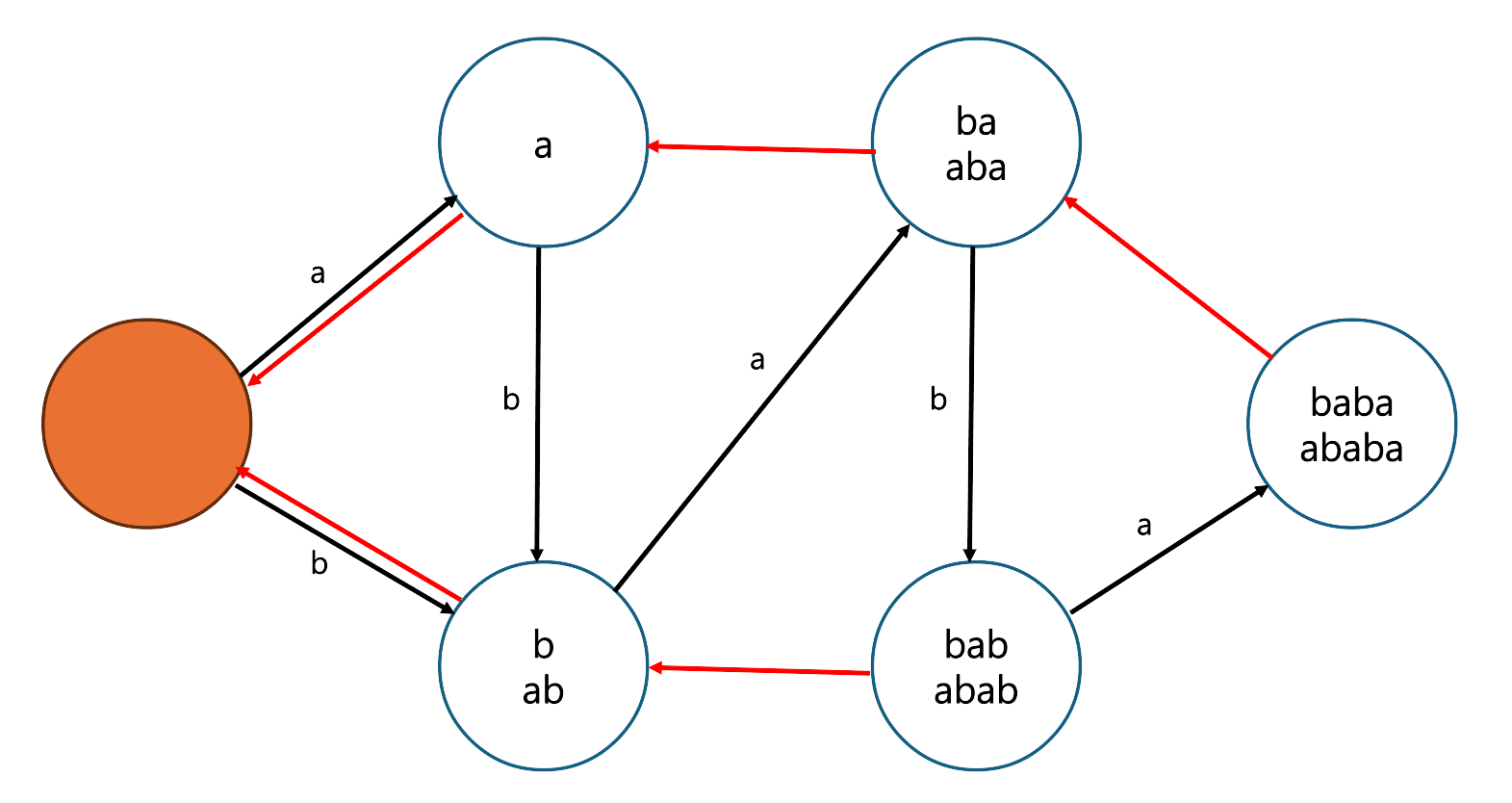
루트를 제외한 모든 상태에서 출발하는 suffix link가 단 하나 있다. 즉, suffix automaton에서 suffix link만 놓고 보면 트리 구조를 이루고 그 트리는 $S$를 뒤집은 문자열의 Suffix Tree가 된다! 해당 suffix tree에서는 suffix automaton의 상태에 있는 문자열 중 길이가 가장 긴 문자열이 상태가 된다. 그래서 suffix automaton만 공부하면 따로 Ukkonen알고리즘을 배울 필요 없이 Suffix Tree를 구할 수 있다. 뒤에서 보겠지만 suffix automaton도 Ukkonen알고리즘처럼 incremental 하기때문에 유사한 방식으로 문제를 해결할 수 있다.

Algorithm
이제 우린 suffix automaton을 구할 준비가 됐다. 각 상태에 저장해야 하는 정보는 다음과 같다.
- 다음 상태로 가는 간선
- 현재 상태에서 가장 긴 문자열의 길이
- suffix link 상태 번호
suffix automaton을 구하는 알고리즘은 incremental한 알고리즘이므로 다음 과정은 문자 하나 $c$에 대해 동작한다. 즉, 다음 과정은 $S$를 나타내는 suffix automaton 에서 $S + c$를 나타내는 suffix automaton을 구해준다.
- 새로운 상태를 만들고 현재 상태를 가장 긴 문자열을 가진 상태로 둔다.
- 현재 상태에서 $c$를 값으로 가지는 간선을 연결한다.
- 현재 상태를 suffix link를 타고 내려간 상태로 대체하며 해당 상태가 루트이거나 값이 $c$인 간선이 이미 존재할 때까지 위 과정을 반복한다.
이 과정에서 suffix link를 타고 내려가는 모든 상태들은 $c$가 추가되기 전 문자열의 suffix들이기 때문에 각 suffix들에 대해 간선을 연결해주는 작업이다.
이제 위의 과정을 모두 마쳤다면 어떠한 상태$p$에 도달했을 텐데 $p$는 루트이거나 아닐 것이다.
$p$가 루트인 경우
$S + c$의 suffix중 하나도 $S$의 부분문자열이 아니라는 뜻이므로 suffix link는 루트가 된다.
$p$가 루트가 아닌 경우
$S + c$의 suffix중 하나가 $S$의 부분문자열로 존재했다는 뜻이다.
상태 $p$의 가장 긴 문자열을 $P$라고 하고 해당 문자열의 길이를 $len(p)$라고 하자.
$len(p) + 1 = len(p + c)$라면 새로운 상태의 suffix link는 $P + c$가 있는 상태가 된다. (상태 $p$에서 간선 $c$를 따라 간 상태)
그렇지 않다면 상태 $p + c$를 복사하고 해당 상태를 $clone$이라고 하자. $len(clone)$의 값을 $len(P) + 1$로 둔다. 그 후 새로운 상태의 suffix link는 $clone$이 된다. 마지막으로 상태 $p$에서 suffix link를 타고 내려가며 만나는 상태마다 $c$로 나가는 간선을 모두 $clone$으로 보낸다.
Problems
https://www.acmicpc.net/problem/16916
원래 KMP같은 패턴매칭 알고리즘 연습문제로 주어진 문제지만 세상이 빠르게 변하고 있어 파이썬의 in이나 C++의 substr로 해결할 수 있게 되어 난이도가 수직하락한 문제이다. 부분문자열을 체크하는 문제는 $S$에 대한 suffix automaton을 구성하고 $P$를 accept하는지 확인하면 된다.
문자열 관련 알고리즘은 하나같이 어렵고 복잡하다. 그나마 Suffix Automaton이 이해하기 쉬운 편인 것 같으니 시간 나면 다시 한번 deep dive를 해봐야겠다.
References
https://cp-algorithms.com/string/suffix-automaton.html
https://codeforces.com/blog/entry/20861
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] PS를 위한 Splay Tree (1) | 2024.10.03 |
|---|---|
| [알고리즘] Pollard rho 알고리즘 (0) | 2024.09.28 |
| [알고리즘] Push Relabel 알고리즘 (2) | 2024.08.30 |
| [알고리즘] Berlekamp-Massey 알고리즘 톺아보기 (2) | 2024.07.24 |
| [알고리즘] 현대모비스 알고리즘 경진대회 2024 후기 (2) | 2024.07.07 |